Przemysław Janicki, Sr Pre-Sales Solutions Architect, Risk Solutions GSZ/CE, SAS

Obliczenia kwantowe (ang. quantum computing) to szybko rozwijająca się dziedzina badań stosowanych o potencjalnie dużej zdolności rozwiązywania złożonych problemów i wykonywania obliczeń bądź to wykraczających poza granice możliwości klasycznych komputerów, jakie towarzyszą nam od dziesięcioleci, przetwarzających porcje informacji w sposób deterministyczny (dodając dwa do dwóch tysiące razy zawsze otrzymamy cztery) przy użyciu tranzystorów i bramek logicznych, bądź też – z powodów, o których za chwilę – nigdy dla nich nieosiągalnych.

Komputery kwantowe do przetwarzania informacji wykorzystują osiągnięcia mechaniki kwantowej. Jest to dziedzina fizyki o fundamentalnym wręcz dziś znaczeniu, która wyjaśnia zachowanie oraz oddziaływania materii i energii w najmniejszych skalach, takich jak atomy i cząstki subatomowe, choć jej początki sięgają pierwszych dekad XX wieku i osiągnięć takich pionierów teorii kwantowej jak Max Planck, Albert Einstein, Niels Bohr czy Erwin Schrödinger, które to osiągnięcia – głównie w domenie teoretycznej i eksperymentalnej – kilkadziesiąt lat później (od mniej więcej lat 80. XX wieku) zostały przestawione na tory praktycznych zastosowań w dziedzinie obliczeniowej przez fizyków w rodzaju Richarda Feynmana czy Davida Deutscha (współautora pierwszego algorytmu kwantowego po raz pierwszy opublikowanego w 1992 r.), do których niebawem dołączyli matematycy i informatycy tacy jak Peter Shor (autor słynnego algorytmu faktoryzacji, czyli rozkładu liczby na czynniki pierwsze, 1994), Aleksiej Kitajew (który zaproponował algorytm szybkiej kwantowej transformacji Fouriera, 1995) czy Lov Grover (kwantowy algorytm przeszukiwania baz danych, 1995).

Dlaczego komputery kwantowe są potrzebne

Richard Feynman, uznawany za jednego z największych fizyków naszych czasów, w jednym ze swoich wykładów wygłoszonych w California Institute of Technology (Caltech) w Pasadenie („Simulating Physics with Computers”, ogłoszonego w formie artykułu), półtorej dekady po przyznaniu mu w 1965 r. Nagrody Nobla za niezależne stworzenie relatywistycznej elektrodynamiki kwantowej, zadał pytanie: „Czy układ kwantowy może być probabilistycznie symulowany przez klasyczny (nawet gdyby był probabilistyczny) komputer uniwersalny?”. Innymi słowy, czy coś z natury kwantowego może być symulowane przez komputer, który nie jest kwantowy? Już w kolejnym zdaniu dał odpowiedź: „Jeżeli przyjmiemy, że komputer jest komputerem klasycznym (…), że żadne prawa nie ulegają zmianie i nie wchodzi w grę żadne hokus-pokus, odpowiedź z pewnością brzmi: nie!”.

Przyczyny tak kategorycznej odpowiedzi zostały przez Feynmana – wybitnego naukowca i świetnego dydaktyka zarazem, hołdującego własnej wersji brzytwy Ockhama, zwanej techniką Feynmana: jeżeli potrafisz coś wytłumaczyć w prosty sposób, to znaczy, że naprawdę to rozumiesz – natychmiast wyjaśnione: mamy do czynienia z problemem ukrytych zmiennych (ang. the hidden-variable problem), który sprawia, że nie da się przedstawić wyników mechaniki kwantowej za pomocą klasycznego komputera uniwersalnego. Uzasadnienie tej tezy znajdziemy w piątej części przywołanego artykułu Richarda Feynmana, a sprowadza się ono, z grubsza rzecz biorąc, do ukazania swoistej odmienności świata i towarzyszących mu zjawisk na poziomie kwantowym, gdzie istnieją „immanentne indeterminizmy” wynikające głównie ze słynnej zasady nieoznaczoności Wernera Heisenberga. Można też powiedzieć (w duchu Feynmana upraszczania tego, co skomplikowane), że stan układu fizycznego nie daje jego pełnego opisu, co w zasadzie automatycznie wyklucza z pewnych zastosowań klasyczne komputery deterministyczne, niezależnie od ich mocy.

Kwantowa dominacja

Wszystko to nie musi jednak prowadzić do wniosku, że komputery kwantowe będą musiały zastąpić komputery oparte na klasycznej architekturze, gdyż w przypadku wielu codziennych zadań, takich jak przeglądanie zasobów internetu, przetwarzania tekstu czy obróbki filmów, standardowe komputery wciąż mogą się okazać wystarczająco wydajne, a na pewno znacznie mniej… kosztowne. Autorzy pierwszych algorytmów kwantowych uświadomili nam po prostu, że komputery kwantowe teoretycznie mogą przewyższać komputery klasyczne w niektórych zadaniach, sam zaś Richard Feynman uświadomił nam wiele lat wcześniej, że niektórych zagadnień o potencjalnie doniosłym znaczeniu dla całej ludzkości po prostu nie będziemy w stanie rozwiązać bez wsparcia ze strony komputerów kwantowych.

Do pierwszej grupy możemy zaliczyć różnego rodzaju zagadnienia symulacyjne i optymalizacyjne (choćby bardzo praktyczne i „przyziemne” zagadnienie wyceny instrumentów finansowych czy optymalizacji składu portfela inwestycyjnego), ale też, wspomniane już, algorytmy faktoryzacji, które mają bezpośrednie przełożenie na nasze bezpieczeństwo z uwagi na to, jak działa współczesna kryptografia. W ogólnym zarysie proces rozkładu dowolnie dużej liczby na czynniki pierwsze stanowi na tyle trudne wyzwanie dla komputerów klasycznych, że od dziesięcioleci stanowi punkt wyjścia w popularnych protokołach bezpieczeństwa takich jak TLS czy RSA, a także technologii łańcucha bloków (ang. blockchain) i opartych na niej rozwiązań, jak kryptowaluty w rodzaju bitcoina. TLS i RSA chronią przed nieupoważnionym dostępem znaczną część codziennego ruchu w internecie, a technologia blockchain oferuje integralność i bezpieczeństwo przechowywanych danych, m.in. zapewniając nienaruszalność i transparentność historii transakcji kryptowalutami (i nie tylko nimi).

Do drugiej grupy problemów moglibyśmy zaliczyć te, które mają naturę kwantową, co w świetle przytoczonego wykładu Richarda Feynmana powoduje, że klasyczne komputery nigdy nie pozwolą nam ich rozwiązać. Według aktualnego stanu wiedzy moglibyśmy zaliczyć tutaj poznanie natury tak fundamentalnych dla życia na Ziemi zjawisk jak fotosynteza, czy dalszy rozwój chemii obliczeniowej, który mógłby skutkować nie tylko obniżeniem kosztów wytwarzania i testowania nowych leków, ale docelowo mógłby doprowadzić do rozwoju medycyny w pełni spersonalizowanej, a więc odzwierciedlającej fizjologię indywidualnego pacjenta i jej specyfikę. Z pewnością przyczynią się też do wynalezienia nowych rewolucyjnych materiałów. W obszarze sztucznej inteligencji komputery kwantowe mogą pomóc w optymalizacji uczenia modeli, potencjalnie prowadząc do powstania bardziej inteligentnych i wydajnych systemów AI – już dziś generatywna sztuczna inteligencja potrafi wiele, dlatego możemy sobie wyobrazić, ile by mogła zdziałać, gdybyśmy dysponowali znacznie większą mocą obliczeniową, skracającą proces uczenia niektórych modeli językowych z tygodni czy miesięcy do interwału wyrażanego w sekundach. Również problemy takie jak modelowanie klimatu wymagają ogromnej mocy obliczeniowej ze względu na ogromną złożoność układów klimatycznych, więc i w tym zastosowaniu unikalne możliwości obliczeniowe komputerów kwantowych mogą umożliwić nam wydajną ich symulację, prowadząc nie tylko do dokładniejszych prognoz, ale i do głębszego zrozumienia zmian klimatu, których przecież doświadczamy.

Wnioski uzyskane z tych symulacji być może pozwolą nam odpowiedzieć ostatecznie na ciągle sporne, zdaniem wielu, pytanie, czy obserwowane zmiany klimatu mają charakter wyłącznie antropogeniczny, tym samym pomagając nam lepiej kształtować odpowiedzialną politykę i kreować bardziej zrównoważoną przyszłość. Te i inne wątki są rozważane w przystępny sposób m.in. przez H. Noaha w jego książce „21 lekcji na XXI wiek” (Wydawnictwo Literackie) czy w ujęciu nieco bardziej technicznym przez M. Kaku w książce „Kwantowa dominacja. Jak komputery kwantowe odmienią nasz świat” (wydawnictwo Prószyński Media). Ale nawet te stosunkowo nieliczne podane wyżej przykłady powinny nam uświadomić jak duże znaczenie może mieć dla każdego z nas kwantowa dominacja (ang. quantum supremacy), czyli moment, w którym przy pomocy komputerów kwantowych ostatecznie pokonamy bariery dalszego rozwoju komputerów klasycznych. I nie chodzi nawet o to, że już przy obecnym stanie technologii klasyczne komputery potrzebowałyby miliardów lat na rozwiązanie niejednego z problemów, który komputer kwantowy mógłby rozwiązać dosłownie w przeciągu chwili, ale o to, że powoli zbliżamy się do kresu technologicznych możliwości dalszej miniaturyzacji układów scalonych i idącej w ślad za nią zwiększania mocy obliczeniowej współczesnych komputerów.

Ograniczenia komputerów klasycznych

W ogólnym zarysie współczesne komputery oparte są na dużej liczbie tranzystorów, które możemy wyobrażać sobie jako pewien rodzaj przełącznika. Oznacza to, że tranzystor może znajdować się w jednym z dwóch stanów: włączonym (w zapisie cyfrowym reprezentowanym przez 1) lub wyłączonym (0). Ta informacja o stanie jest znana jako bit i jest najmniejszą jednostką informacji przetwarzanej przez komputer. Zadania jakie stawiamy przed naszymi komputerami są jednak dużo bardziej złożone i aby je zrealizować musimy połączyć wiele bitów, a zatem wykorzystać dużą liczbę tranzystorów. Im więcej bitów w komputerze, tym więcej informacji może on przetworzyć. Dlatego moc obliczeniowa klasycznych komputerów zależy przede wszystkim od technicznych możliwości upakowania miliardów tranzystorów na płytce drukowanej w postaci układów scalonych, a więc w praktyce od naszej zdolności do miniaturyzacji tranzystorów, która jednak ma swoje fizyczne granice. Znanym tego odzwierciedleniem jest obecny stan tzw. prawa Moore’a, które przewidywało systematyczne podwajanie liczby tranzystorów w układzie scalonym (a więc i mocy obliczeniowej komputerów) przy minimalnym nakładzie kosztów, ceteris paribus, a które – zdaniem coraz większej liczby ekspertów – na naszych oczach się dezaktualizuje.

Doświadczenia ostatnich lat mogą sugerować, że zbliżyliśmy się już do momentu, w którym przy obecnym stanie technologii dalszy istotny przyrost mocy obliczeniowej może znajdować się poza naszym zasięgiem. A jeżeli się odbędzie, to nie bez istotnego wzrostu nakładów – technologie produkcyjne nowej generacji, takie jak Extreme Ultraviolet Lithography (litografia w ekstremalnym ultrafiolecie, EUV), są bowiem drogie i wymagają wysoce specjalistycznego sprzętu, przez co producentom coraz trudniej jest osiągać korzyści skali, które wcześniej sprawiały, że prawo Moore'a tak dobrze się sprawdzało. Jak sugeruje pionier (klasycznej) techniki komputerowej Gene Amdahl w swoim wywodzie (nazwanym później prawem Amdahla), nie będziemy w stanie obejść tych ograniczeń przez szersze stosowanie układów wieloprocesorowych (wielowątkowych) i przetwarzania równoległego, gdyż wzrost szybkości wykonywania się klasycznego algorytmu komputerowego przy użyciu większej liczby procesorów w obliczeniach równoległych jest ograniczany nie tylko prawami fizyki, ale przez sekwencyjny podział algorytmu (i w efekcie jakiejś jego części nie da się zrównoleglić). Nawet jeżeli aż 95% kodu mogłoby być przetwarzane równolegle, wówczas maksymalny wzrost szybkości jego wykonania przy użyciu przetwarzania równoległego nie przekroczy 20-krotności poziomu odniesienia – i to bez względu na liczbę użytych procesorów (por. Rysunek 1).

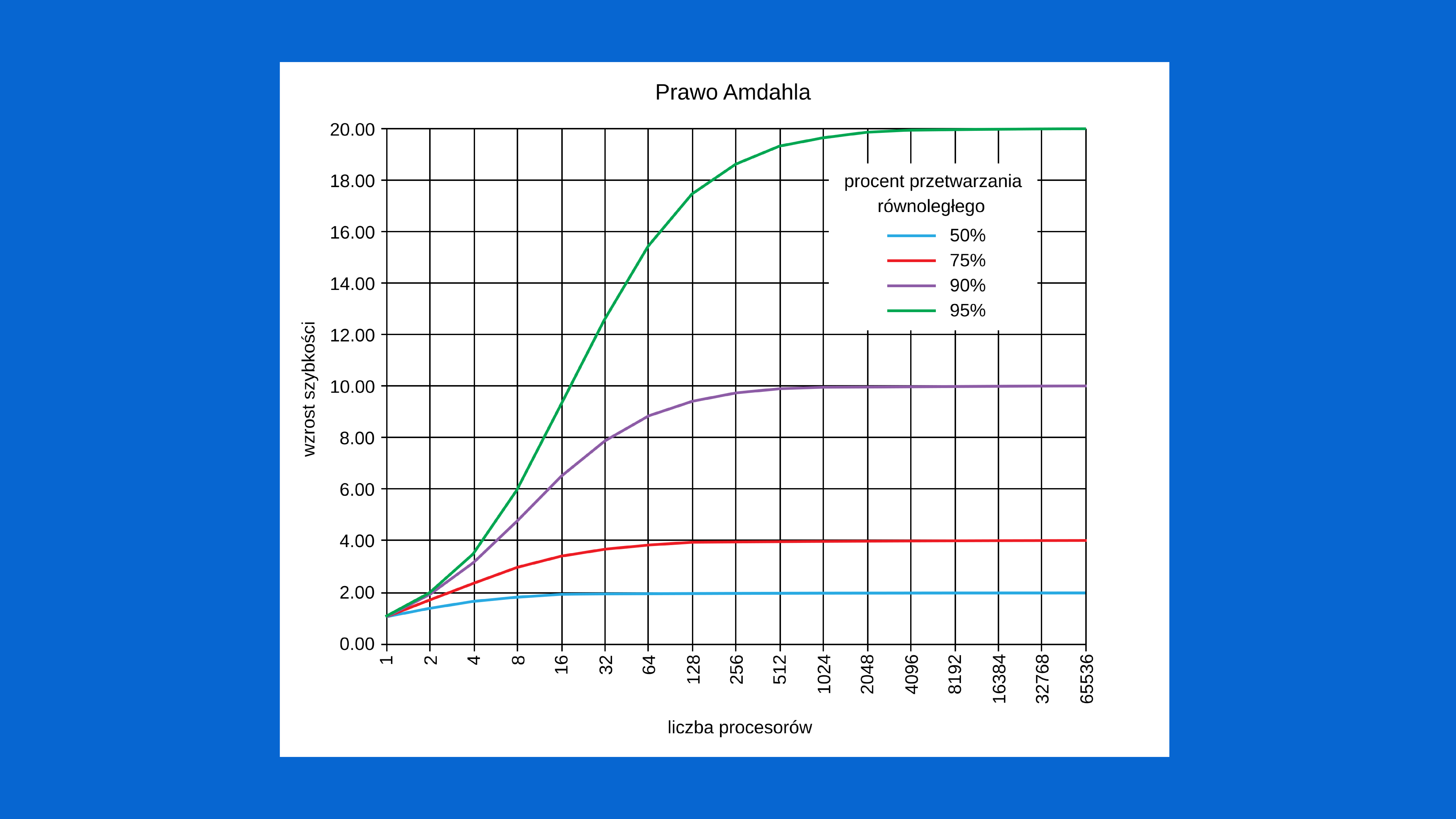
Rysunek 1. Wizualizacja prawa Amdahla (źródło: Wikipedia)

Natura obliczeń kwantowych

W przeciwieństwie do komputerów klasycznych, które operują na porcjach informacji zwanych bitami, komputery kwantowe wykorzystują tzw. bity kwantowe, czyli kubity (ang. qubits). Są one podobne jedynie z nazwy: kubity, dzięki wykorzystaniu takich zjawisk jak superpozycja czy splątanie kwantowe, pozwalają komputerom kwantowym wykonywać pewne obliczenia w sposób całkowicie odmienny, a przy tym znacznie szybciej niż najszybsze komputery klasyczne kiedykolwiek będą w stanie. Superpozycja pozwala kubitom reprezentować wiele stanów jednocześnie (a nie tylko logiczne stany 0 i 1 – przypomnij sobie znany eksperyment myślowy, a zarazem paradoks, kota Schrödingera), a splątanie tworzy szczególnego rodzaju stan skorelowania między kubitami (stan kubitu wpływa na stan kubitu z nim splątanego), co łącznie czyni komputery kwantowe tak wydajnymi w realizacji pewnego typu zadań (Albert Einstein był akurat tak sceptycznie nastawiony do idei splątania kwantowego, że nazwał je „upiornym działaniem na odległość”). Ale też powoduje, że algorytmy kwantowe i programowanie komputerów kwantowych różnią się fundamentalnie od swych klasycznych odpowiedników.

Kubity mają przy tym wady, a jedną z poważniejszych jest to, że w przeciwieństwie do klasycznych bitów są podatne na błędy przez swoją wrażliwość na warunki zewnętrzne. Nawet niewielka zmiana temperatury lub zakłócenia elektromagnetyczne mogą wpłynąć na stan kubitu, a korekcja błędów w komputerach kwantowych jest szczególnie trudna, ponieważ pomiar stanu kubitu może go zmienić (co więcej, fundamentalne dla mechaniki kwantowej twierdzenie o braku klonowania – ang. no-cloning theorem – stanowi, że nie da się wiernie skopiować informacji kwantowej). Obecnie opracowywane są różne techniki korekcji błędów, ale nadal pozostaje to jedną z największych barier w rozwoju obliczeń kwantowych, gdyż – jak zobaczymy za chwilę – korekcja może znacząco zwiększyć wymaganą liczbę kubitów ponad niezbędną do rozwiązania zagadnienia podstawowego (gdyby kubity nie były podatne na błędy). Wszystkie te aspekty sprawiają, że projektowanie algorytmów, które mogą efektywnie wykorzystywać takie zjawiska jak superpozycja czy splątanie kwantowe, wymaga odmiennego rodzaju myślenia i dobrego zrozumienia mechaniki kwantowej (a także m.in. algebry, liczb zespolonych czy rachunku prawdopodobieństwa). Dlatego jest to ciągle jeszcze umiejętność niszowa, na którą jednak popyt powinien tylko rosnąć.

Tworzenie i testowanie algorytmów z pewnością ułatwiają biblioteki i frameworki stanowiące rozszerzenie popularnych języków programowania, jak choćby IBM Qiskit, gdzie do tworzenia obwodów kwantowych (ang. quantum circuit) wykorzystujemy składnię języka Python (a same obwody mogą być uruchamiane na emulatorach lub rzeczywistych komputerach kwantowych). Rysunek 2 przedstawia wizualizację przykładowego obwodu stworzonego na potrzeby implementacji algorytmu Shora realizującego podział na dwa czynniki liczby 15, którego pełen opis znajdziemy na stronie: https://quantum.cloud.ibm.com/docs/en/tutorials/shors-algorithm

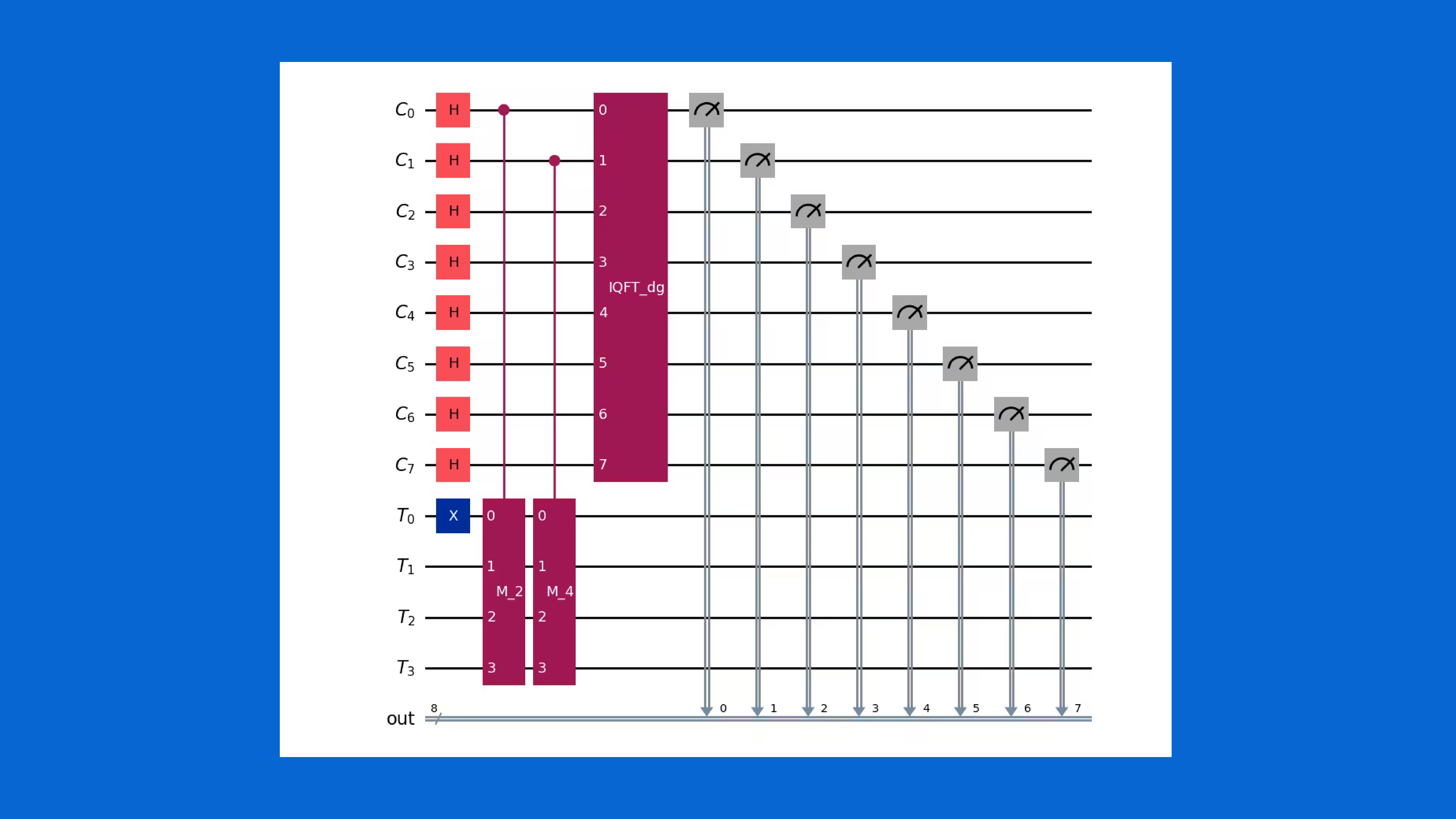
Rysunek 2. Przykładowy obwód kwantowy zaimplementowany przy użyciu frameworku IBM Qiskit (źródło: IBM)

Praktyczna implementacja algorytmu Shora przez IBM po raz pierwszy miała miejsce w 2001 r. na komputerze kwantowym typu NMR (ang. nuclear magnetic resonance) o 7 kubitach. Od tego czasu nastąpił znaczny postęp w fizycznej realizacji komputerów kwantowych. Jak jednak zauważa sam IBM w dającym do myślenia przykładzie, szyfrowanie RSA zazwyczaj wymaga już kluczy o długości rzędu 2048-4096 bitów. Próba rozłożenia liczby 2048-bitowej za pomocą algorytmu Shora na czynniki pierwsze wymusi powstanie obwodu kwantowego z milionami kubitów, wliczając w to narzut na korekcję błędów (gdyby nie ona, wystarczyłoby ich, jak się szacuje, 4000-6000). To przekracza realne możliwości obecnych komputerów kwantowych. Dlatego w celu praktycznego zastosowania algorytmu Shora do przełamania zabezpieczeń kryptograficznych będzie on wymagał zoptymalizowanych metod budowy obwodów lub znacznie wydajniejszej korekcji błędów. To nie tylko interesujące wyzwanie intelektualne, ale i zagadnienie o potencjalnie doniosłych skutkach dla świata jaki znamy i w jakim żyjemy.

Era NISQ

W zrozumieniu gdzie jesteśmy dzisiaj pomaga skala opracowana przez firmę Microsoft, znana jako Quantum Computing Implementation Levels. Wszystko wskazuje na to, że obecnie ciągle jeszcze znajdujemy się w tzw. erze Noisy Intermediate Scale Quantum (NISQ), czyli na stosunkowo wczesnym etapie rozwoju technologii kwantowych, kiedy to komputery kwantowe są wciąż stosunkowo małe i podatne na błędy, z drugiej jednak strony możemy być świadkami bardzo dynamicznego ich rozwoju (por. Rysunek 3). Nie zmieniają tego (jeszcze) pojawiające się niekiedy pogłoski – ze strony tej czy innej firmy budującej własnej komputery kwantowe – o osiągnięciu dominacji kwantowej.

Rysunek 3. Trzy ery (poziomy) rozwoju komputerów kwantowych według Microsoft (źródło: Microsoft Quantum).

O ile komputery kwantowe są cały czas podatne na błędy, kwestia tego, na ile obecne komputery kwantowe możemy nazwać „stosunkowo małymi” może być w pewnym sensie dyskusyjna – nie da się bowiem postępu w rozwoju techniki oddzielić od postępów w rozwoju algorytmiki, które przecież następują również niezależnie od siebie. Jedyne co możemy dziś zrobić, to zweryfikować ją częściowo przez zestawienie topowych urządzeń istniejących dziś z szacunkami IBM na temat mocy (wyrażonej liczbą kubitów) niezbędnej do złamania algorytmu RSA. Według stanu na dziś do miana najbardziej precyzyjnego komputera kwantowego pretenduje Helios (stworzony przez Quantinuum, w której to spółce udziały nabyła Nvidia czy bank inwestycyjny JPMorgan Chase), największą liczbą kubitów może się poszczycić urządzenie stworzone w Caltech (tym samym, w którym pracował Richard Feynman), złożone z sieci 6100 kubitów, zaś w niektórych zadaniach najwydajniejszy okazuje się być chiński komputer oparty na nadprzewodzącym chipie Zuchongzhi-3. Najbliższa przyszłość pokaże, jak szybko będziemy mogli dowieść, że przeszliśmy do kolejnej ery w implementacji tej wiele obiecującej technologii. Warto przy tym pamiętać, że już dziś (w erze NISQ) pojawiają się opinie, iż przed 2030 r. złamanie 2048-bitowego klucza RSA będzie możliwe. W tym wyścigu każdy z nas może wziąć udział jako twórca ulepszonych algorytmów.